Keyboard shortcuts

Press ← or → to navigate between chapters

Press S or / to search in the book

Press ? to show this help

Press Esc to hide this help

Quick start

Installation

See the Installation section.

Create a project

Create a new project with this command:

cargo creusot new project-name

Note

If you are using the development version of Creusot (master branch), you should also point your project to your local copy of creusot-contracts, using the --creusot-contracts option (otherwise the default is to use the released version on crates.io). To avoid hard-coding local paths in your configuration, one approach is to set --creusot-contracts creusot-contracts, and make a symbolic link creusot-contracts pointing to your local creusot-contracts.

That command creates a directory package-name containing the basic elements of a Rust project verified with Creusot. The file src/lib.rs is initialized with an example function annotated with a contract:

// src/lib.rs
use creusot_contracts::prelude::*;

#[requires(x@ < i64::MAX@)]
#[ensures(result@ == x@ + 1)]
pub fn add_one(x: i64) -> i64 {
    x + 1
}

Compile and prove

To verify this project, run this command:

cargo creusot prove

A successful run gives us the certainty that functions defined in this package satisfy their contracts: for all arguments satisfying the preconditions (requires clauses), the result of the function will satisfy the postconditions (ensures clauses).

The command cargo creusot prove does two things: compile your Rust crate to Coma, then search for proofs of verification conditions generated from the Coma code using Why3find. These steps can be performed separately.

  1. Run only the compiler and obtain Coma code:

    cargo creusot

  2. Run Why3find’s proof search only on a specific Coma file (by default, Why3find is run on all Coma files under the verif):

    cargo creusot prove verif/[COMA_FILE]

    Multiple files can also be specified in a single command.

When the proof fails, you can add the -i option to open the Coma file in Why3 IDE.

cargo creusot prove verif/[COMA_FILE] -i

The -i option only launches the Why3 IDE if the proof fails. You can also use --ide-always

cargo creusot prove verif/[COMA_FILE] --ide-always

When you know that the proof is going to fail, it can be slow to update every time you modify your code. To skip proof search and just reuse the existing proof.json as is, add the option --replay.

cargo creusot prove verif/[COMA_FILE] --ide-always --replay

The documentation for the Why3 IDE can be found here.

We also recommend section 2.3 of this thesis for a brief overview of Why3 and Creusot proofs.

Troubleshooting

If you get an error like this

error: The `creusot_contracts` crate is loaded, but the following items are missing: <a list of identifiers> Maybe your version of `creusot-contracts` is wrong?

Add the following to your Cargo.toml file:

[patch.crates-io]
creusot-contracts = { path = "/relative/or/absolute/path/to/creusot-contracts/in/creusot/directory" }

And please notify the Creusot developers that the version of Creusot should be bumped to NEXT_VERSION-dev to prevent this error.

Legacy workflow with Why3 IDE

This workflow is intended to help projects using old versions of Creusot that still use why3session.xml.

Run the Creusot compiler:

cargo creusot

Launch the Why3 IDE:

cargo creusot why3 ide [FILE]

You must specify a file why3session.xml or a Coma file.

Difference with cargo creusot prove:

  • cargo creusot prove (with -i or --ide-always) runs the Creusot compiler and the Why3find proof search beforehand, ensuring that you’re always working on the latest version of your code.
  • cargo creusot why3 ide only runs why3 ide with the necessary options to load Coma files produced by Creusot. It’s up to you to make sure that the Coma files are up-to-date.

Editor configuration

From the root of your project, write the following in the .vscode/settings.json file:

{
  "rust-analyzer.check.overrideCommand": [
    "cargo",
    "creusot",
    "--",
    "--message-format=json"
  ]
}

For other editors, see https://rust-analyzer.github.io/book/other_editors.html to add the above option to your configuration.

Note that you will probably want to enable this option only in projects that use creusot.

Installation

This section explains how to install Creusot, what goes into the installation, and some configuration options.

Quick installation (using custom script)

The INSTALL script installs Creusot and its accompanying tools.

Requirements to run the INSTALL script:

  • cargo
  • opam to install why3 and why3find.
  • curl to download provers: alt-ergo, z3, cvc4, cvc5.
./INSTALL

See ./INSTALL --help for options.

Note that the INSTALL script will take a couple minutes to create a local Opam switch and then to install the many dependencies of why3.

The local switch will be located in $XDG_DATA_HOME/creusot/_opam (default on Linux: ~/.local/share/creusot/_opam). We recommend having this local switch to prevent accidentally breaking your Creusot setup while working on other OCaml projects.

Quick installation (using nix)

If you are using nix, you do not need to have a copy of this repository.

We assume that you have nix installed on your system. Setup instructions can be found here: https://nixos.org/download

You can use nix shell to enter an interactive subshell containing the project:

nix shell "github:creusot-rs/creusot"

The project lives in this subshell and will disappear as soon as you leave the subshell.

If you do not have flakes enabled, you may get this error:

error: experimental Nix feature 'nix-command' is disabled; use ''--extra-experimental-features nix-command' to override

All you have to do is activate flakes temporarily by using --extra-experimental-features 'nix-command flakes':

nix --extra-experimental-features 'nix-command flakes' shell "github:creusot-rs/creusot"

Manual installation

  1. You can install the core files from the Creusot repository with Cargo alone:

    # Install cargo-creusot
cargo install --path cargo-creusot

# Install creusot-rustc
TOOLCHAIN=$(grep "nightly-[0-9-]*" --only-matching rust-toolchain)
cargo install --path cargo-creusot --root $XDG_DATA_HOME/creusot/toolchain/$TOOLCHAIN/bin

# Install the Creusot prelude with Why3find
cargo run --bin prelude-generator
(cd target && why3find install --global creusot)

# Copy why3find.json in the installation directory
cp cargo-install/why3find.json $XDG_DATA_HOME/creusot/why3find.json

  2. The following binaries must then be put in $XDG_DATA_HOME/creusot/bin, refer to their respective project pages for how to get them:

    • why3 (available on Opam)
    • why3find (available on Opam)
    • alt-ergo (downloadable binaries, also on Opam)
    • z3 (downloadable binaries, also on Opam)
    • cvc5 (downloadable binaries)
    • cvc4 (downloadable binaries)

Installed files

Everything Creusot needs to run.

  • cargo-creusot in PATH. This is the entry point of Creusot.

  • $XDG_DATA_HOME/creusot/ (default on Linux: ~/.local/share/creusot), a directory containing:

    • toolchain/$TOOLCHAIN/bin/creusot-rustc, the Creusot compiler, where $TOOLCHAIN is the toolchain used to build Creusot (set by the file rust-toolchain in the Creusot repository).

    • bin/ containing binaries.

      • why3 and why3find
      • Provers: alt-ergo, z3, cvc5, cvc4

    • why3find.json, which is used to create new Creusot projects with cargo creusot new or cargo creusot init.

  • The Creusot prelude, a Why3find package (with the local switch from the Quick installation, on Linux, the prelude is located at ~/.local/share/creusot/_opam/lib/why3find/package/creusot).

Why3

The Why3 configuration is located at $XDG_CONFIG_HOME/creusot/why3.conf (default on Linux: ~/.config/creusot). This file is generated by cargo creusot prove if it does not already exist, and by cargo creusot why3-conf. Notable options in this file:

  • the location and version of provers ([partial_prover]) (for the Nix installation, this is not known during the installation of Creusot, that’s why this file is generated later).
  • The maximum number of parallel prover jobs (running_provers_max = ...).
  • [strategy] for solving goals in Why3 IDE.
  • [ide] options for Why3 IDE (can be modified in the menu File > Preferences).

Why3find

cargo creusot prove invokes why3find, which looks for the file why3find.json in the current working directory or one of its parents. At the moment we recommend not modifying why3find.json. Instead, you should rely on adapting your Rust code to make proofs more robust, for example by adding more assertions. Please open an issue if this configuration does not work for you.

Nevertheless, you may like to experiment with some of these options:

  • "fast" and "time": timeout durations in seconds for provers.
  • "depth": proof search is pruned after this number of levels.
  • "tactics": list of tactics to apply during proof search. “Tactics” are Why3 transformations that take no arguments. For example: compute_in_goal and inline_goal are tactics; apply H, exists X are not tactics.

See the Why3find README for more information.

Tutorial

This tutorial is an introduction to deductive verification with Creusot. After introducing basic concepts, we will walk through the steps to verify a function with Creusot.

No prior knowledge about formal methods is required to follow this tutorial. Basic familiarity with Rust should be enough to get started with Creusot.

Creusot

Follow the README to install Why3 and Creusot.

Setup

Create a new project with this command:

cargo creusot new creusot-tutorial

This generates a directory creusot-tutorial containing the following files:

Cargo.toml
why3find.json
src/lib.rs

The first two files contain package-level configuration settings. You’re most likely already familiar with Cargo.toml. why3find.json is used by a verification tool invoked by Creusot. We will leave these files alone for this tutorial.

The last file, src/lib.rs, is what we will be editing in this tutorial.

My first contract

Open src/lib.rs. It contains an example function with a contract:

use creusot_contracts::prelude::*;

#[requires(x@ < i64::MAX@)]
#[ensures(result@ == x@ + 1)]
pub fn add_one(x: i64) -> i64 {
    x + 1
}

In Creusot, contracts are how we specify the expected behavior of functions. A contract contains two kinds of assertions: preconditions, or “required clauses”, describe the values of arguments that the function accepts; postconditions, or “ensured clauses”, describe the result value that the function returns.

In this first example, there is one precondition (requires) and one postcondition (ensures). This contract can be read as follows: if the argument x is smaller than i64::MAX, then the value of add_one(x) will be equal to x@ + 1.

More generally, a function satisfies its contract when, for any input arguments that satisfy the preconditions (requires), the result of the function satisfies the postcondition (ensures).

It is not a very exciting contract, since it just replicates the body of the function x + 1. But note that x@ + 1 is not exactly the same expression. The @ suffix is Creusot’s view operator, which maps a Rust value to a mathematical value. If x has type i64, then x@ has type Int, as the type of mathematical integers (…, -2, -1, 0, 1, 2, …). The key difference is that mathematical integers are unbounded: their arithmetic operations do not overflow. They are more intuitive and better behaved than operations on machine integer. For example, all x: Int satisfy x < x + 1 whereas this cannot be true for Rust’s machine integers because they are finite.

The type Int is one of several built-in types of common mathematical objects defined by Creusot; others include sequences and mappings (mathematical functions). On the one hand, mathematical objects like Int cannot be manipulated by Rust programs, they can only be used in contracts. On the other hand, values that exist in Rust programs such as machine integers (i64, etc.) are not as easy to manipulate in the logical world of contracts, so we use the view operator @ to transform them into something more intuitive.

The contract of add_one specifies the result slightly indirectly: its view as an unbounded integer, denoted by result@, must be equal to x@ + 1. Note that arithmetic operations are only defined on Int in the logical world of contracts.

Verifying the contract

cargo creusot prove

First, the Rust code is compiled to Coma, an intermediate verification language in the Why3 platform. Second, Why3 verifies the compiled program by generating verification conditions and sending them as queries to SMT solvers. When all verification conditions have been proved, that amounts to proving that functions defined in our crate satisfy their contracts.

My second contract

Here is a more involved example: given a non-negative integer n, compute the sum of all integers between 0 and n included. We can do this simply by iterating through each integer up to n. This is the function to verify.

pub fn sum_up_to(n: u64) -> u64 {
    let mut sum = 0;
    let mut i = 0;
    while i < n {
        i += 1;
        sum += i;
    }
    sum
}

Although a for loop would be idiomatic, that also adds some complications to the verification process. For the sake of simplicity, we start with a while loop, and switch to a for loop at the end.

As a sanity check, we can write unit tests:

#[test]
pub fn test_sum_up_to() {
    // 1 + 2 + 3 + 4 = 10
    assert_eq!(sum_up_to(4), 10);
}

Run with

cargo test

Whereas unit tests let us check the output associated with specific inputs of a function, contracts let us specify the output for all possible inputs. Naturally, we can’t exhaustively list input-output pairs. Instead, we describe the relation between inputs and outputs as properties, logical formulas that are true about the inputs and outputs of a function.

Contract

The result of this sum is also known as the triangular numbers, with a well-known formula: n * (n + 1) / 2. This provides a nice and concise specification for sum_up_to.

Write an #[ensures(...)] clause to give a postcondition to sum_up_to using the formula for triangular numbers.

Added postcondition 
#[ensures(result@ == n@ * (n@ + 1) / 2)]
pub fn sum_up_to(n: u64) -> u64 {
    // ...
}

Run cargo creusot to make sure that the postcondition is well-formed. Of course, cargo creusot prove will fail. The contract is still too naive at this point.

What if the sum overflows? Feel free to try different approaches to handle this problem. Here is a non-exhaustive list of possibilities.

Add a simple bound on the input as a precondition 
#[requires(n@ < 1000)]
#[ensures(result@ == n@ * (n@ + 1) / 2)]
pub fn sum_up_to(n: u64) -> u64 {
    // ...
}
Add a more precise upper bound as a precondition 
#[requires(n@ * (n@ + 1) / 2 <= u64::MAX@)]
#[ensures(result@ == n@ * (n@ + 1) / 2)]
pub fn sum_up_to(n: u64) -> u64 {
    // ...
}
Allow overflows and adjust the postcondition accordingly 
#[ensures(result@ == (n@ * (n@ + 1) / 2) % (u64::MAX + 1))]
pub fn sum_up_to(n: u64) -> u64 {
    // ...
}
Change the result type to be big enough 
#[ensures(result@ == n@ * (n@ + 1) / 2)]
pub fn sum_up_to(n: u64) -> u128 {
    // ...
}

At this point, you may have a contract that is satisfied by the function, but cargo creusot prove still can’t verify it. This function contains a loop, and loops must be annotated with loop invariants: assertions which must be true at every iteration of the loop.

Loop invariants

A loop invariant looks like this:

    #[invariant(i@ <= n@)]
    while i < n {
        i += 1;
        sum += i;
    }

At every step, i is less than or equal to n. In particular, it is true when we enter the loop (when i = 0), inside the loop body it must have been that i < n, which gives us i+1 <= n, with i+1 as the next value of i, and when we exit, the loop condition i < n is false, which combined with the invariant i@ <= n@ tells us that i = n when the function returns. We could have written this invariant as i <= n, without the @.

Inspecting proofs with Why3 IDE

The invariant is still incomplete. To investigate what’s missing, we can inspect proofs in progress with Why3 IDE. The command cargo creusot prove with the -i option launches Why3 IDE, showing the proof state for an as yet unverified function.

cargo creusot prove -i

If there are many functions to verify, we can pick a specific one on the command line by naming the Coma file it was compiled to. Coma files are generated in the verif/ directory, and their path consists of the crate name (creusot_tutorial_rlib for the library creusot-tutorial) followed by the fully qualified function name (creusot_tutorial::sum_up_to becomes creusot_tutorial/sum_up_to.coma).

cargo creusot prove -i verif/creusot_tutorial_rlib/creusot_tutorial/sum_up_to.coma

Why3 IDE is a GUI that looks like this:

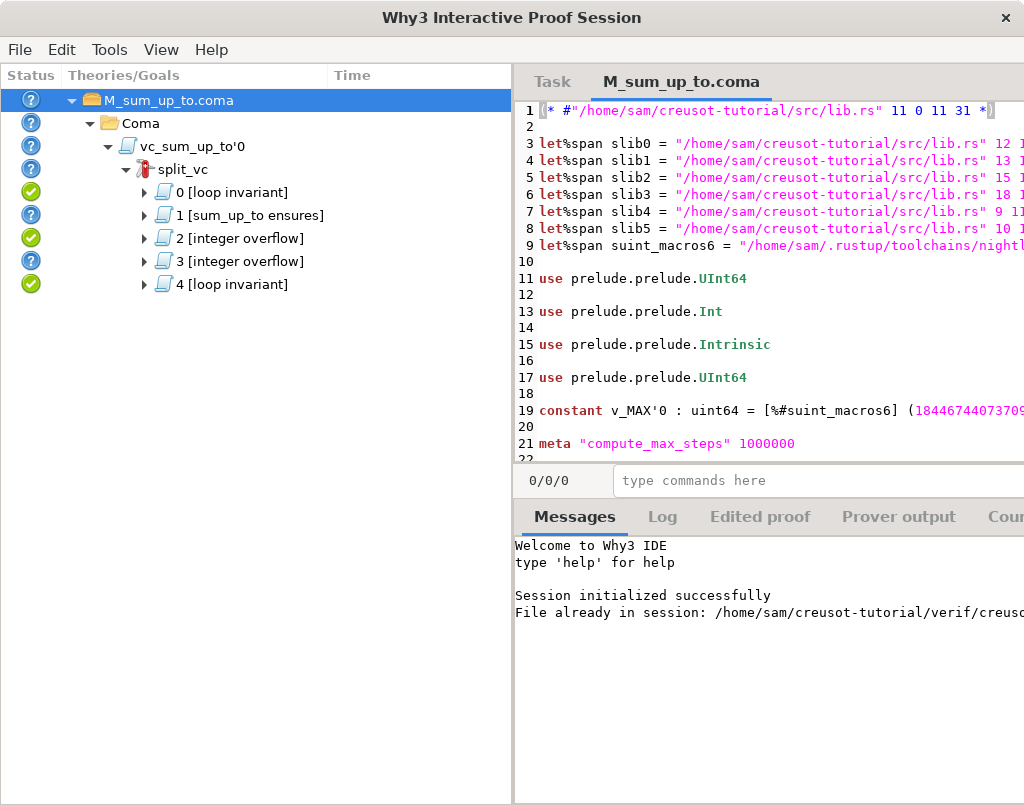
Screenshot of Why3 IDE window

It’s a three-pane window. The left panel displays the tree of goals to prove. The top right panel displays the proof context, which consists of relevant source files and a special Task tab listing available hypotheses and the goal formula. The bottom right panel contains error messages and other logs.

In the left panel, the status of every tree node is shown as an icon in the leftmost column. Goals with complete proofs have green checkmarks, unproved goals have blue question marks. Currently, the bottom of the tree consists of five subgoals labeled [loop invariant], [sum_up_to ensures], [integer overflow] twice, and [loop invariant] again.

To verify that a function satisfies its contract, Why3 generates verification conditions which represent properties that must hold at certain points in the program:

  1. Starting from the top of the function sum_up_to, we must check that the loop invariant holds when we enter the loop, that corresponds to the first [loop invariant] goal.

  2. Inside the loop, we show that any iteration of the loop body preserves the loop invariant: we start with arbitrary values of i and sum assuming that the loop invariant holds and that the condition i < n is true. Checking that i += 1 does not overflow corresponds to the first [integer overflow] goal. Checking that sum += i does not overflow corresponds to the second [integer overflow] goal.

  3. At the end of the loop body the invariant must hold again, corresponding to the last [loop invariant] goal.

Finally, at the loop exit, we assume that the loop invariant holds and that the condition i < n is false, and prove that the returned value satisfies the postcondition (ensures clause), which corresponds to the [sum_up_to ensures] goal. It may seem surprising that the goal [sum_up_to ensures] appears first even though it corresponds to the end of the function; this is due to internal details of compiling the program to a control-flow graph and generating verification conditions by traversing the control-flow graph in a somewhat arbitrary order.

One way to make sense of the goals is to look at the source spans they contain. In the left panel, click on the goal labeled [sum_up_to ensures]. That opens a tab lib.rs on the top right panel; click on it.

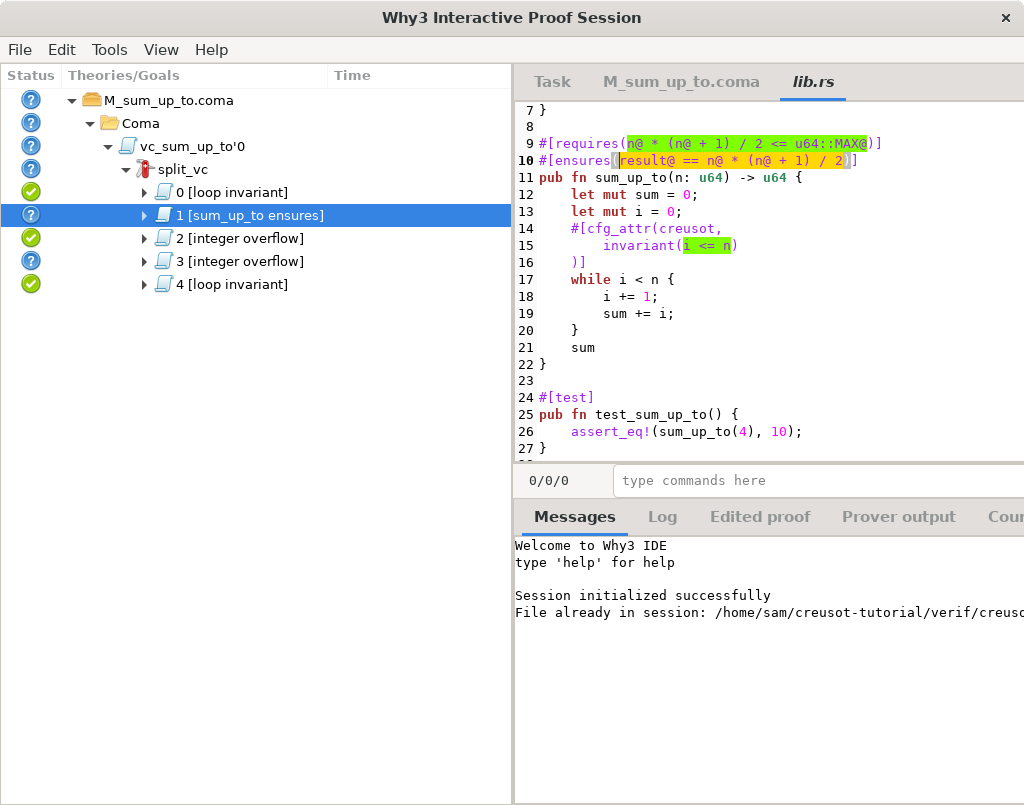
Screenshot of Why3 IDE window, focused on ensures goal

We see a view of the Rust code we are trying to verify, with highlighted spans relevant to the goal we selected. What we are trying to prove is highlighted in yellow: the goal [sum_up_to ensures], as its name indicates, is trying to prove that the ensures clause holds when the function returns. Hypotheses and various bits of code that the goal depends on are highlighted in green: the requires clause and the loop invariant are hypotheses.

Similarly, you can inspect the two [loop invariant] goals. Both will highlight the invariant i <= n in yellow, but there will be a difference in the surrounding spans: one goal will highlight the 0 from the initialization of i, indicating that the goal comes from entering the loop, whereas the other goal will highlight the 1 in the increment i += 1, indicating that the goal comes from checking that the loop body maintains the loop invariant.

It is easy to prove that the addition in i += 1 will not overflow, because the loop condition i < n is true. However we cannot deduce that the addition in sum += i will not overflow yet, because we know nothing about sum in the loop invariant. For that same reason, there is also no way to prove the postcondition ([sum_up_to ensures]).

Complete the loop invariant

Complete the invariant. Below we extended the invariant with a placeholder for your solution. Intuitively, the invariant should reflect the idea that at every step, sum is the sum of numbers from 0 to i included.

    #[invariant(i@ <= n@)]
    #[invariant(true /* YOUR INVARIANT HERE */)]
    while i < n {
        i += 1;
        sum += i;
    }
Completed invariant 
    #[invariant(i@ <= n@)]
    #[invariant(sum@ == i@ * (i@ + 1) / 2)]
    while i < n {
        i += 1;
        sum += i;
    }

With that, cargo creusot prove succeeds. We have proved that the function sum_up_to satisfies its contract.

Complete sum_up_to function with all annotations 
#[requires(n@ * (n@ + 1) / 2 <= u64::MAX@)]
#[ensures(result@ == n@ * (n@ + 1) / 2)]
pub fn sum_up_to(n: u64) -> u64 {
    let mut sum = 0;
    let mut i = 0;
    #[invariant(i@ <= n@)]
    #[invariant(sum@ == i@ * (i@ + 1) / 2)]
    while i < n {
        i += 1;
        sum += i;
    }
    sum
}

Use a for loop

The while loop above can be replaced with a more idiomatic for loop.

    for i in 1..=n {
        sum += i;
    }

Verifying a for loop is more complicated because we must reason about iterators. Another challenge is that the invariant cannot talk about the next value (i): there might not be a next value.

Creusot defines a special variable, produced, which contains the sequence of elements previously produced by the iterator of a for loop. Using that variable, we can restate the invariant about sum:

    #[invariant(sum@ == produced.len() * (produced.len() + 1) / 2)]
    for i in 1..=n {
        sum += i;
    }

Indeed, produced.len() is exactly the number of past iterations.

We no longer need the other clause of the invariant, i <= n, first because i isn’t even in scope in the invariant, and also because that fact will be deduced automatically from the postcondition of next for the iterator 1..=n, which is where i comes from.

We are almost done. In principle, that invariant should be all we need to complete the proof. But the solvers can’t figure it out for some reason. It may be that solvers have trouble with division. We can tweak the invariant to avoid relying on division, and the proof goes through.

    #[invariant(sum@ * 2 == produced.len() * (produced.len() + 1))]
    for i in 1..=n {
        sum += i;
    }

This kind of wrinkle is par for the course in SMT-based tools such as Creusot.

Complete sum_up_to function with all annotations (for loop version) 
#[requires(n@ * (n@ + 1) / 2 <= u64::MAX@)]
#[ensures(result@ == n@ * (n@ + 1) / 2)]
pub fn sum_up_to(n: u64) -> u64 {
    let mut sum = 0;
    #[invariant(sum@ * 2 == produced.len() * (produced.len() + 1))]
    for i in 1..=n {
        sum += i;
    }
    sum
}

Conclusion

In this tutorial, we’ve got a glimpse of the workflow of verifying a Rust program in Creusot.

We have only scratched the surface. Creusot offers many more features for verifying Rust code at large. You can read about them in the rest of this user guide.

Basic concepts

Every Creusot macro will erase themselves when compiled normally: they only exist when using cargo creusot.

If you need to have Creusot-only code, you can use the #[cfg(creusot)] attribute.

Note that you must explicitly use the creusot_contracts crate in your code (which should be the case once you actually prove things, but not necessarily when you initially set up a project), such as with the line:

use creusot_contracts::prelude::*;

or you will get a compilation error complaining that the creusot_contracts crate is not loaded.

requires and ensure

Most of what you will be writing with creusot will be requires and ensures clauses. That is: preconditions and postconditions.

Together, those form the contract of a function. This is in essence the “logical signature” of your function: when analyzing a function, only the contract of other functions is visible.

Preconditions with requires

A precondition is an assertion that must hold when entering the function. For example, the following function accesses a slice at index 0:

fn head(v: &[i32]) -> i32 {
    v[0]
}

So we must require that the slice has at least one element:

#[requires(v@.len() >= 1)]
fn head(v: &[i32]) -> i32 {
    v[0]
}

Note the view (@) operator: it is needed to convert the Rust type &[i32] to a logical type Seq<i32>. Else, we could not call [T]::len, which is a program function (and not a logical one).

To learn more, see the chapter on Pearlite and Views.

Postconditions with ensures

A postcondition is an assertions that is proven true at the end of the function. The return value of the function can be accessed via the result keyword.

In the case of the example above, we want to assert that the returned integer is the first of the slice:

#[requires(v@.len() >= 1)]
#[ensures(v@[0] == result)]
fn head(v: &[i32]) -> i32 {
    v[0]
}

Note that we:

  • use the @ operator on the slice to get a Seq<i32>
  • we can then index this Seq<i32> to get a i32.

Invariants

When writing a loop (be it for, while or loop), you will generally need to specify an invariant, that is an assertion that stays true for the duration of the loop. For example, the following program:

#[ensures(result == n)]
fn loop_add(n: u64) -> u64 {
    let mut total = 0;
    while total < n {
        total += 1;
    }
    total
}

Needs an invariant: even though its proof seems obvious to us, it is not for Creusot. What Creusot knows is:

  • Any variable not referenced in the loop is unchanged at the end (here this is obvious because n is immutable, but it might be relevant in a more complicated program).
  • At the end of the loop, the loop condition is false: here total >= n.

We still need to know that total <= n to get result == n:

#[ensures(result == n)]
fn loop_add(n: u64) -> u64 {
    let mut total = 0;
    #[invariant(total <= n)]
    while total < n {
        total += 1;
    }
    total
}

This is now provable !

Like requires and ensures, invariant must contain a pearlite expression returning a boolean.

Verification conditions

An invariant generates two verification conditions in Why3:

  • First, that the invariants holds before the loop (initialization).
  • Second, that if the invariant holds at the beginning of a loop iteration, then it holds at the end of it.

Compiling with rustc

Make sure that functions that contain #[invariant(...)] attributes also have an #[ensures(...)] or #[requires(...)] attribute. You can always add #[ensures(true)] as a trivial contract.

That enables compilation (cargo build) with a stable Rust compiler, preventing the following error:

error[E0658]: attributes on expressions are experimental

Indeed, the #[invariant(...)] attribute on loops is only allowed by unstable features (stmt_expr_attributes, proc_macro_hygiene). For compatibility with stable Rust, the requires and ensures macros remove #[invariant(...)] attributes during normal compilation.

Variants

A variant clause can be attached either to a function like ensures, or requires or to a loop like invariant, it should contain a strictly decreasing expression which can prove the termination of the item it is attached to.

proof_assert!

At any point in the code, you may want to insert an arbitrary verification condition. This can be useful:

  • For debugging, to ensure that a property indeed holds at a certain point of the program.
  • To help the provers in specific cases.

To do this, Creusot gives you the proof_assert! macro:

fn f() {
    // ...
    let x = 1;
    let y = 2;
    proof_assert!(x@ + y@ == 3);
    // ...
}

proof_assert must contain a pearlite expression returning a boolean.

Trusted

The trusted marker lets Creusot trust the implementation and specs. More specifically, you can put #[trusted] on a function like the following:

#[trusted]
#[ensures(result == 42u32)]
fn the_answer() -> u32 {
    trusted_super_oracle("the answer to life, the universe and everything")
}

TODO: trusted traits

Representation of types

Creusot translates Rust code to Why3. But Rust types don’t always exist in Why3, and would not have the same semantics: thus we need to map each Rust type to a Why3 type.

Base types

Most type have a very simple interpretation in Why3:

  • The interpretation for a scalar type (i32, bool, f64, …) is itself.

  • The interpretation of [T] is Seq<T>, the type of sequences.

  • The interpretation of &T is the interpretation of T.

    Creusot is able to assume that T and &T behave the same, because of the “shared xor mutable” rule of Rust: we won’t be able to change the value (interior mutability is handled by defining a special model for e.g. Cell<T>), so we may as well be manipulating an exact copy of the value.

  • The interpretation of Box<T> is the interpretation of T.

    This is because a Box uniquely own its content: it really acts exactly the same as T.

  • Structures and enums are interpreted by products and sum types.

  • The interpretation of &mut T is a bit more complicated: see the next section.

Mutable borrows

In Creusot, mutable borrows are handled via prophecies. A mutable borrow &mut T contains:

  • The current value (of type T) written in the borrow.
  • The last value written in the borrow, called the prophecy.

This works in the underlying logic by performing two key steps:

  • When the borrow is created, the prophecy is given a special any value. We don’t know it yet, we will trust the logic solvers to find its actual value based on later operations.
  • When dropping the borrow, Creusot adds the assumption current == prophecy. We call that resolving the prophecy.

Final reborrows

The above model is incomplete: in order to preserve soundness (see the Why is this needed ? section), we need to add a third field to the model of mutable borrows, which we call the id.

Each new mutable borrow gets a unique id, including reborrows. However, this is too restrictive: with this, the identity function cannot have its obvious spec (#[ensures(result == input)]), because a reborrow happens right before returning.

To fix this, we introduce final reborrows:

A reborrow is considered final if the prophecy of the original borrow depends only on the reborrow. In that case, the reborrow id can be inherited:

  • If this is a reborrow of the same place (e.g. let y = &mut *x), the new id is the same.
  • Else (e.g. let y = &mut x.field), the new id is deterministically derived from the old.

Examples

In most simple cases, the reborrow is final:

let mut i = 0;
let borrow = &mut i;
let reborrow = &mut *borrow;
// Don't use `borrow` afterward
proof_assert!(reborrow == borrow);

#[ensures(result == x)]
fn identity<T>(x: &mut T) -> &mut T {
    x
}

It even handles reborrowing of fields:

let mut pair = (1, 2);
let mut borrow = &mut pair;
let borrow_0 = &mut borrow.0;
proof_assert!(borrow_0 == &mut borrow.0);

However, this is not the case if the original borrow is used after the reborrow:

let mut i = 0;
let borrow = &mut i;
let reborrow = &mut *borrow;
*borrow = 1;
proof_assert!(borrow == reborrow); // unprovable
                                   // Here the prophecy of `borrow` is `1`,
                                   // which is a value completely unrelated to the reborrow.

Or if there is an indirection based on a runtime value:

let mut list = creusot_contracts::vec![1, 2];
let borrow: &mut [i32] = &mut list;
let borrow_0 = &mut borrow[0];
proof_assert!(borrow_0 == &mut borrow[0]); // unprovable

Why is this needed ?

In essence, to prevent the following unsound code:

pub fn unsound() {
    let mut x: Snapshot<bool> = snapshot! { true };
    let xm: &mut Snapshot<bool> = &mut x;
    let b: &mut Snapshot<bool> = &mut *xm;
    let bg: Snapshot<&mut Snapshot<bool>> = snapshot! { b };
    proof_assert! { ***bg == true && *^*bg == true };
    let evil: &mut Snapshot<bool> = &mut *xm;
    proof_assert! { (evil == *bg) == (*^evil == true) };
    *evil = snapshot! { if evil == *bg { false } else { true } };
    proof_assert! { **evil == !*^evil };
    proof_assert! { **evil == !**evil };
}

If borrows are only a pair of current value/prophecy, the above code can be proven, and in particular it proves **evil == !**evil, a false assertion.

Pearlite

Pearlite is the language used in:

  • contracts (ensures, requires, invariant, variant)
  • proof_assert!
  • the pearlite! macro

It can be seen as a pure, immutable fragment of Rust which has access to a few additional logical operations and connectives. In practice you have:

  • Base Rust expressions: matching, function calls, let bindings, binary and unary operators, tuples, structs and enums, projections, primitive casts, and dereferencing
  • Logical Expressions: quantifiers (forall and exists), logical implication ==>, logical equality a == b, labels
  • Rust specific logical expressions: access to the final value of a mutable reference ^, access to the view of an object @

Logical implication

Since => is already a used token in Rust, we use ==> to mean implication:

proof_assert!(true ==> true);
proof_assert!(false ==> true);
proof_assert!(false ==> false);
// proof_assert!(true ==> false); // incorrect

Quantifiers

The logical quantifiers ∀ and ∃ are written forall and exists in Pearlite:

#[requires(forall<i: Int> i >= 0 && i < list@.len() ==> list@[i] == 0)]
fn requires_all_zeros(list: &[i32]) {
    // ...
}

Logic functions

Functions marked with #[logic] can be used in specifications (requires/ensures and invariant) and in snapshot!, but cannot be called from normal Rust code. Typically, logic functions manipulate variables of logical model types such as Int and Seq<Int> rather than normal Rust types such as i32 and &[i32].

Logical function use normal Rust syntax, but the operators are the logical ones: == in a #[logic] function does not mean PartialEq::eq, but is rather logical equality. The full pearlite syntax can be used by opening a pearlite! { ... } block.

Logical functions can only call other logical functions, not program functions (and vice-versa).

The #[logic] attribute may take additional modifiers in parentheses, like #[logic(open, prophetic)]. Those attributes are described in the following subsections.

Recursion

When you write recursive logical functions, you have to show that the function terminates.

There are two ways to do so:

  • If the recursion has a structural variant, you have nothing to do. A structural variant is when you match on a value, and only use sub-parts of the match in the recursive call:

    enum List { Nil, Cons(Box<Self>) }

#[logic]
fn length(l: List) -> Int {
    match l {
        List::Nil => 0,
        List::Cons(tail) => 1 + length(*tail),
    }
}

    In this case, the recursion is accepted by Why3 automatically.

  • Else, you need to add a #[variant(EXPR)] attribute to the function. Creusot will then check that the expression EXPR strictly decreases (in a known well-founded order) at each recursive call.

    The type of EXPR should implement the WellFounded trait.

Examples

Basic example:

#[logic]
fn logic_add(x: Int, y: Int) -> Int {
    x + y
}

#[requires(x < i32::MAX)]
#[ensures(result@ == logic_add(x@, 1))]
pub fn add_one(x: i32) -> i32 {
    x + 1
}

Pearlite block:

#[logic]
fn all_ones(s: Seq<i32>) -> bool {
    pearlite! {
        forall<i: Int> i >= 0 && i < s.len() ==> s[i]@ == 1
    }
}

#[ensures(all_ones(result@))]
#[ensures(result@.len() == n@)]
pub fn make_ones(n: usize) -> Vec<i32> {
    creusot_contracts::vec![1; n]
}

Recursion:

TODO

Prophetic:

TODO

Visibility of logical functions

By default, logic functions are opaque outside the module they are defined in (in other words, they are only open at the module level). When a function is opaque, only its pre- and postconditions are visible. This is useful if the function is only used to express (and prove) that the preconditions imply the postconditions, and we do not care about the result (a lemma 1). However, if you do want to use the result in a specification outside the module (e.g. if you are using it as a predicate in one or more contracts), you use the open modifier. It takes an optional argument, similar to pub, e.g. you could specify that a function is to be #[logic(open(super))] or #[logic(open(crate))].

mod inner {
    // ensures in needed here, as code outside the module will not see the body
    // of this function
    #[ensures(result == x + 1)]
    #[logic]
    pub fn adds_one_closed(x: Int) -> Int { x + 1 }

    // no need for `ensures` here!
    #[logic(open)]
    pub fn adds_one_open(x: Int) -> Int { x + 1 }
}

Additionally, you can use the opaque modifier to make the logical function fully opaque, even to other functions in the module. In this case, you cannot attach a specification to the function: you only know that it returns some value (note that this is sound, as all types are inhabited in the logic). This is one of the only places where you can use the dead special keyword, which does nothing but indicate that the function has no implementation.

#[logic(opaque)]
fn generate_int() -> Int {
    dead
}

  1. The Dafny tutorial is a pretty good resource on how to use lemmas. ↩

Prophetic functions

As seen in the chapter on mutable borrow, a mutable borrow contains a prophetic value, whose value depends on future execution. In order to preserve the soundness of the logic, #[logic] functions are not allowed to observe that value: that is, they cannot call the prophetic ^ operator.

If you really need a logic function to use that operator, you need to mark it with #[logic(prophetic)] instead. In exchange, this function cannot be called from snapshot!.

A normal #[logic] function cannot call a #[logic(prophetic)] function.

Lemmas and laws

Lemmas

A lemma is a logical function that is useful because of its pre and postconditions, rather than the value it returns.

For example, suppose that as part of a proof, we want to prove that x + y > 0 ==> x > 0 || y > 0. We can define it as a logical function:

#[logic]
#[requires(x + y > 0)]
#[ensures(x > 0 || y > 0)]
fn add_gt_zero(x: Int, y: Int) {}

This lemma is easily proved by SMT solvers, so we don’t need to give it a body. Sometimes though, it may be useful to define a body to guide the proof: in this toy example, we could do

#[logic]
#[requires(x + y > 0)]
#[ensures(x > 0 || y > 0)]
fn add_gt_zero(x: Int, y: Int) {
    if x > 0 {} else {
        proof_assert!(y >= x + y);
    }
}

If x > 0, the proof is over; else, we know by arithmetic that y >= x + y, so by transitivity of the order it must be > 0.

Lemmas as trait properties

A lot of traits impose greater constraint on their operation than can be seen in the type system.

In this case, additional constraint may be defined as lemmas. For example, we may want to define a trait for commutative operations:

trait Commutative: Sized {
    #[logic]
    fn op(self, other: Self) -> Self;

    #[logic]
    #[ensures(self.op(other) == other.op(self))]
    fn commutative(self, other: Self);
}

To ensure commutativity in a way that makes it easy on implementors, we define it as an additional lemma commutative. Implementors of this trait must then prove that commutativity holds for any self and other.

Laws

The above example has a potential issue: when using op, we don’t automatically know that it is commutative: we have to use the lemma first, to import it into the proof context:

#[logic]
fn foo<T: Commutative>(x: T, y: T) {
    let z = x.op(y);
    // let _ = x.commutative(y);
    proof_assert!(z == y.op(x)); // does not work without uncommenting the above line
}

To make this easier, we can define commutativity as a law: a logical function that will get imported into the context whenever a function in the same trait is used.

trait Commutative: Sized {
    #[logic]
    fn op(self, other: Self) -> Self;

    #[logic(law)]
    #[ensures(self.op(other) == other.op(self))]
    fn commutative(self, other: Self);
}

#[logic]
fn foo<T: Commutative>(x: T, y: T) {
    let z = x.op(y);
    proof_assert!(z == y.op(x)); // Works!
}

Views as models of types

It is generally convenient to map a Rust type to its logical model. This logical model is the type that specifications and clients then use to describe values of this type in the logic.

In Creusot, this is provide using the creusot_contracts::View trait, providing a view method mapping the type to a ViewTy associated type for the model.

Specifications can then use the @ operator as a syntactic sugar for .view() on a type that implements View.

For example, the following gives a spooky data type MyPair<T, U> a nice pair model.

struct MyPair<T, U> {
  fst: T,
  snd: U,
}

impl<T, U> View for MyPair<T, U> {
    type ViewTy = (T, U);

    #[logic(open)]
    fn view(self) -> Self::ViewTy {
        (self.fst, self.snd)
    }
}

#[ensures(result@ == (a, b))]
fn my_pair<T, U>(a: T, b: U) -> MyPair<T, U> {
    MyPair(a, b)
}

Termination

By default, Creusot does not require that program functions terminate, which may lead to surprising situations:

#[ensures(result@ == 42)]
fn nonsense() -> u64 {
    while true {}
    1
}

This can be avoided at the cost of more complicated verification, by adding the check(terminates) attribute to a function:

#[check(terminates)]
#[ensures(result@ == 42)]
fn nonsense() -> u64 { // Fails to compile now !
    while true {}
    1
}

A function with the check(terminates) attribute cannot:

  • Call a non-terminates function.

  • Use a loop construct (for, while, loop). This restriction may be lifted in the future.

  • Use simple recursion without the variant attribute.

    This means that this function will not be accepted:

    #[check(terminates)]
fn f(x: u32) -> bool {
    if x == 0 { false } else { f(x - 1) }
}

    But this one will (the variant will be checked by why3):

    #[check(terminates)]
#[variant(x)]
fn f(x: u32) -> bool {
    if x == 0 { false } else { f(x - 1) }
}

  • Use mutual recursion, like in the following example:

    #[check(terminates)]
fn f() { g() } // Error: mutually recursive functions

#[check(terminates)]
fn g() { f() }

Mutual recursion through traits

Traits complicate the recursion analysis. Indeed, if we have a function like

trait Tr {
    fn f();
}
fn g<T: Tr>() {
    <T as Tr>::f();
}

It isn’t possible to know ahead of time which instance of f will be called.

Thus, Creusot makes the decision to check recursion at instantiation time: the above example compiles, but

trait Tr {
    fn f();
}
fn g<T: Tr>() {
    <T as Tr>::f();
}

impl Tr for i32 {
    fn f() {
        g::<i32>();
    }
}

does not, because we know that g::<i32> calls <i32 as Tr>::f(), causing a cycle.

Dependencies

The recursion check explores the body of the functions in the current crate, but it cannot do so with the dependencies, whose function bodies are not visible.

Thus, it assumes two things:

  1. The recursion check passed on the dependencies of the current crate.
  2. If a function in a dependency has a trait bound, the recursion check pessimistically assumes that all the functions of the trait are called.

Example:

// dependency/src/lib.rs
trait Tr {
    fn f();
}
fn g<T: Tr>() {
    // It does not matter if `<T as Tr>::f` is called or not, since we cannot see it
}

// lib.rs
impl Tr for i32 {
    fn f() {
        g::<i32>(); // Error !
    }
}

Snapshots

A useful tool to have in proofs is the Snapshot<T> type (creusot_contracts::Snapshot). Snapshot<T> is:

  • a zero-sized-type
  • created with the snapshot! macro
  • whose model is the model of T
  • that can be dereferenced in a logic context.

Example

They can be useful if you need a way to remember a previous value, but only for the proof:

#[ensures(array@.permutation_of((^array)@))]
#[ensures(sorted((^array)@))]
pub fn insertion_sort(array: &mut [i32]) {
    let original = snapshot!(*array); // remember the original value
    let n = array.len();
    #[invariant(original@.permutation_of(array@))]
    #[invariant(...)]
    for i in 1..n {
        let mut j = i;
        #[invariant(original@.permutation_of(array@))]
        #[invariant(...)]
        while j > 0 {
            if array[j - 1] > array[j] {
                array.swap(j - 1, j);
            } else {
                break;
            }
            j -= 1;
        }
    }

    proof_assert!(sorted_range(array@, 0, array@.len()));
}

#[logic]
fn permutation_of(s1: Seq<i32>, s2: Seq<i32>) -> bool {
    // ...
}
#[logic]
fn is_sorted(s: Seq<i32>) -> bool {
    // ...
}

Ghost code

Sometimes, you may need code that will be used only in the proofs/specification, that yet still obeys the typing rules of Rust. In this case, snapshots are not enough, since they don’t have lifetimes or ownership.

This is why there exists a separate mechanism: ghost code.

ghost! and Ghost<T> are the counterparts of snapshot! and Snapshot<T>.

ghost! blocks

At any point in the code, you may open a ghost! block:

ghost! {
    // code here
}

In ghost! block, you may write any kind of Rust code, with the following restrictions :

  • ghost code must terminate (see termination for details)
  • all functions called must have the #[check(ghost)] attribute
  • When reading an outer variable, the variable must be of type Ghost<T>, or implement Copy
  • When writing an outer variable, the variable must be of type Ghost<T> or Snapshot<T>
  • The output of the ghost! block will automatically be wrapped in Ghost::new

Those restriction exists to ensure that ghost code is erasable: its presence or absence does not affect the semantics of the actual running program, only the proofs.

Ghost<T>

The Ghost<T> type is the type of “ghost data”. In Creusot, it acts like a Box<T>, while in normal running code, it is an empty type. It has the same View as the underlying type, meaning you can use the @ operator directly.

The only restriction of Ghost<T> is that it may not be dereferenced nor created in non-ghost code.

Examples

  • Creating and modifying a ghost variable:
let mut g = ghost!(50);
ghost! {
    *g *= 2;
};
proof_assert!(g@ == 100);
  • Calling a function in ghost code:
#[check(ghost)]
#[requires(*g < i32::MAX)]
#[ensures((^g)@ == (*g)@ + 1)]
fn add_one(g: &mut i32) {
    *g += 1;
}

let mut g = ghost!(41);
ghost! {
    add_one(&mut *g);
};
proof_assert!(g@ == 42);
  • Using a ghost access token:
struct Token;

struct Data {
    // ...
}

impl Data {
    fn new() -> (Data, Ghost<Token>) { /* */ }
    fn read(&self, token: &Ghost<Token>) -> T { /* */ }
    fn write(&self, t: T, token: &mut Ghost<Token>) { /* */ }
}

Ghost structures

Using imperative data structures in ghost code

Usual imperative structures like Vec, HashMap or HashSet cannot be used in ghost code. To be precise, you may notice that functions like Vec::push are not marked with the #[check(ghost)] attribute, and so they cannot be called in ghost code.

This is because this function (and other like it) allocate memory, which on the actual machine, is finite. This currently translates to a possible inconsistency when using Vec in ghost code:

use creusot_contracts::{proof_assert, ghost};
ghost! {
    let mut v = Vec::new();
    for _ in 0..=usize::MAX as u128 + 1 {
        v.push(0);
    }
    proof_assert!(v@.len() <= usize::MAX@); // by definition
    proof_assert!(v@.len() > usize::MAX@);  // uh-oh
}

This case might be forbidden in the future by adding a stronger precondition to Vec::push, but the point still stands: the capacity of a ghost vector should be infinite.

Ghost structures

As such, ghost code uses the mathematical structures Seq, FMap and FSet, and adds program functions onto them.

The above snippet becomes:

use creusot_contracts::{proof_assert, ghost, Int, logic::Seq};
ghost! {
    let mut s: Seq<Int> = Seq::new();
    for _ in 0..=usize::MAX as u128 + 1 {
        s.push_ghost(0);
    }
    // proof_assert!(s.len() <= usize::MAX@); // fails
    proof_assert!(s.len() > usize::MAX@);
}

A few things to note:

  • Seq, FMap and FSet are the counterparts for Vec, HashMap and HashSet respectively. They all live in the logic module.
  • Since s in directly the logical type Seq, we don’t need the view operator @.
  • To avoid name clashes, these additional “ghost” functions are almost all suffixed with _ghost. See the documentation for each type to know the available methods, ghost and logical.

Int in ghost

You can manipulate values of type Int in ghost code, by using the int suffix on integer literals:

ghost! {
    let x = 42int;
    let y = 58int;
    assert!(x + y == 100int);
};

Ghost containers return their length as an Int, and Seq is indexed by Int as well:

ghost! {
    let s: Seq<_> = ...;
    let m: FMap<_, _> = ...;
    let len: Int = m.len_ghost();
    let x = s[len + 3int];
};

Type Invariants

Overview

Defining a type invariant allows you to constrain a data type’s set of valid values with a logical predicate that all values must satisfy. During verification, Creusot enforces that all type invariants are preserved across functions. Inside a function, values subject to type invariants may temporarily break their invariants as long as each value’s invariant is restored before the value can be observed by another function.

Type invariants were added to Creusot as part of a Master’s thesis available here.

Defining Type Invariants

To attach an invariant to a type, you implement the Invariant trait provided by Creusot. Here is an example:

struct SumTo10 {
    a: i32,
    b: i32,
}

// The type invariant constrains the set of valid `SumTo10`s to
// only allow values where the sum of both fields is equal to 10.
impl Invariant for SumTo10 {
    #[logic]
    fn invariant(self) -> bool {
        pearlite! {
            self.a@ + self.b@ == 10
        }
    }
}

Enforcement of Type Invariants

Creusot enforces type invariants on function boundaries by generating additional pre- and postconditions based on the types of a function’s arguments and return value. The type invariants of a function’s arguments are treated as additional preconditions and a type invariant of the return value corresponds to an extra postcondition. Here is an example:

// `inv` generically refers to the invariant of some value
#[requires(inv(x))] // generated by Creusot
#[ensures(inv(result))] // generated by Creusot
fn foo(x: SumTo10) -> SumTo10 {
    x
}

These generated pre- and postconditions require you to prove the invariants of any values used as arguments in function calls or returned values. Besides the proof obligations at function boundaries, you must also prove the type invariants of mutably borrowed values when the lifetimes of the created references end. When creating a mutable reference r, Creusot requires you to prove the type invariant of its current value at the end of r’s lifetime, since r might have been used to break the invariant of the borrowed value. This lets Creusot assume the invariant of the final value ^r holds, simplifying the reasoning about mutable references. Here is an example:

fn swap() {
    let mut s = SumTo10 { a: 3, b: 7 }
    let r = &mut s;
    // Creusot can prophetically assume inv(^r) holds:
    proof_assert! { inv(^r) };

    let tmp = r.a;
    *r.a = r.b;
    *r.b = tmp;
    // The lifetime of r ends: We must prove inv(*r)

    proof_assert! { inv(v) }; // provable since v = ^r = *r
}

Structural Invariants

To determine the invariant of a particular type, Creusot considers:

  • User-provided definitions, defined with the Invariant trait.
  • Invariants that can be derived automatically based on the type’s definition.

The second category is called structural invariants. When neither an explicit definition exists, nor a structural invariant, the type has the trivial invariant, which does not impose any constraints on the set of valid values.

Here are some examples demonstrating structural invariants of various types:

Type of xInvariant inv(x)
bool, u8, i32, ...true
&mut Fooinv(*x) && inv(^x)
&Fooinv(*x)
Box<Foo>inv(*x)
*const Foo, *mut Footrue
(Foo, Bar)inv(x.0) && inv(x.1)
struct Foo { f: Bar }inv(x.f)
enum Foo { A(Bar), B(Baz) }match x { A(y) => inv(y), B(z) => inv(z) }
Vec<Foo>inv(x[0]) && ... && inv(x[x.len()-1])

Logical functions

Creusot decides not to add type invariants to the pre- and postconditions of logical functions. This means that the following is not provable:

#[logic]
#[ensures(x.a@ + x.b@ == 10)]
fn no_inv_in_logic(x: SumTo10) {}

Even though the same function in program is provable:

#[ensures(x.a@ + x.b@ == 10)]
fn inv_in_program(x: SumTo10) {}

Erasure check

Verifying functions with Creusot requires modifying their code to add attributes, assertions, ghost code, etc.. This creates a gap between the function that is verified and the function that is compiled and run. The disconnect is two-fold:

  1. The verified function is different from the original function. One may still want to keep using the original function for various reasons, including avoiding a dependency on Creusot.
  2. Even if you compile the verified function, that relies on erasing Creusot annotations, which may affect trait resolution and result in compiling a different function than the one that was verified by Creusot.

To bridge that gap, the #[erasure(...)] attribute maintains a tight connection between the verified function and the original function.

Overview

The attribute #[erasure(f)] is put on a function definition. It asserts that the annotated function f2 (to be verified by Creusot) and the target f (to be compiled) have the same runtime behavior. This is a syntactic check that tries to simply match the bodies of f and f2 with each other modulo small code transformations to ignore purely logical constructs.

#[erasure(f)]
fn f2(x: A) {
    /* ... */
}

The #[erasure] check performs the following operations.

  • Erase Ghost and Snapshot variables, ghost!, snapshot!, and proof_assert! blocks, #[ensures], #[requires], #[invariant] attributes.
  • Replace called functions with their own #[erasure].
  • Equate up to A-normal form.

#[trusted] functions skip the #[erasure] check.

Additional rules for pointers:

Example

Consider the following generic example of “unverified code”. The function h calls two functions f and g:

fn h(x: A) {
    g(f(x))
}

fn f(x: A) -> B { /* ... */ }
fn g(y: B) { /* ... */ }

“Verifying” these functions with Creusot may involve introducing ghost arguments, ghost blocks, assertions, etc., resulting in code that looks as follows.

#[erasure(h)]
#[requires(...)]
#[ensures(...)]
fn h2(x: A) {
    let (y, i) = f2(x);
    ghost!(...);
    g2(y, i)
}

#[erasure(f)]
fn f2(x: A) -> (B, Ghost<I>) { /* ... */ }

#[erasure(g)]
fn g2(y: B, i: Ghost<I>) { /* ... */ }

The attribute #[erasure(h)] checks that h2 behaves the same as the previous h if we ignore ghost code. In order to do this check, Creusot performs a couple of transformations to the body of h.

First, erase ghost blocks, ghost variables, and assertions:

fn h2(x: A) {
    let (y, _) = f2(x);
    g2(y, _)
}

Replace f2 with its erasure f, g2 with its erasure g (as indicated by their own #[erasure] attributes). The erasure of f2 also replaces its result tuple with its only non-ghost component.

fn h2(x: A) {
    let y = f(x);
    g(y)
}

Before comparing h2 and h, we put them both in A-normal form. Here, h2 is simple and already in A-normal form. The body f(g(x)) of the function h gets rewritten as follows.

fn h(x: A) {
    let y = f(x);
    g(y)
}

Now h2 and h are identical, so the #[erasure(h)] check succeeds.

Usage

Intra-crate checks

When #[erasure(f)] mentions a function f defined in the same crate as the annotated function, the erasure check works simply as you would expect.

Cross-crate checks

When #[erasure(f)] mentions a function f from another crate, #[erasure] check failures are reported as warnings by default because they require some setup to work.

The #[erasure] check requires compiling your whole project twice: the first time to know what definitions need to be checked, and the second time to get dependencies to export those definitions. The reason is that #[erasure] compares THIR ASTs, which exist only during the compilation of the crate containing those definitions.

The required definitions are stored as binary blobs in the folder _creusot_erasure so that they persist when removing target/creusot to force a rebuild.

cargo creusot
rm -r target/creusot # Force rebuilding from scratch
cargo creusot --erasure-check

To keep the metadata for #[erasure] checks up to date, you must recompile twice whenever you add new #[erasure] annotations or you update a dependency.

Due to this, #[erasure] checks give different errors depending on whether you have rebuilt your project from scratch at least once (“missing bodies” vs. “the actual check failed”). For that reason, these failures are reported as warnings by default. Use the option --erasure-check to report them as errors instead.

The variants of this option are:

  • --erasure-check=no: disable #[erasure] checks;
  • --erasure-check=warn (default): report #[erasure] check failures as warnings;
  • --erasure-check (or --erasure-check=error): report #[erasure] check failures as errors.

Using core and std

When #[erasure(f)] mentions a function f from core or std, you must use -Zbuild-std to get access to their THIR. Also make sure to have rust-src in your toolchain.

rustup component add rust-src --toolchain $MY_TOOLCHAIN

Private functions

It is also possible to name a private function using the private keyword followed by the full path to the private function:

#[erasure(private crate_name::path::to::f)]

Nested functions

#[erasure] automatically takes nested functions into account.

fn f() {
  fn inside_f() {}
  inside_f()
}

#[erasure(f)]
fn g() {
  fn inside_f() {}
  inside_f()
}

The inner function of g does not need an #[erasure] attribute, but it must have the same name as its counterpart in f.

Ghost functions

Ghost functions are those that may appear outside of ghost blocks but are completely eraseable. The main examples are Ghost::split and Ghost::borrow. They are identified by the attribute #[erasure(_)].

#[trusted]
#[erasure(_)]
fn split<T, U>(g: Ghost<(T, U)>) -> (Ghost<T>, Ghost<U>) { /* ... */ }

Known limitations

Formal verification provides strong guarantees about your code. Nevertheless, it is important to be aware of the limits of what one has specified. Creusot users should take note of the following limitations.

Some panics are allowed

The Vec methods that increase capacity (push, insert, extend, etc.) panic if the capacity overflows. The current contracts in creusot-contracts do not prevent this.

Because Vec is such a fundamental type, bounding its length is quite cumbersome. Moreover, you will probably run out of memory (another kind of failure that Creusot does not prevent) before the capacity overflows. There remains one notable blind spot: a Vec of a zero-sized type enables triggering this panic quite easily.

Architecture specificity

Creusot compiles code for some given target architecture, so the resulting proofs are only valid for that architecture.

An important consequence is that the sizes of many types are constants which depend on the architecture or compiler optimizations. In particular, this affects the value of usize::MAX and the sizes of repr(Rust) types. The latter are technically unspecified by The Rust Reference: Type Layout.

vec! macro

The vec! macro of Rust’s standard library uses special magic to initialize memory slightly more efficiently. Creusot does not support this magic, hence the version provided by the standard library is not supported in Creusot.

Instead, we provide the replacement macro creusot_contracts::std::vec::vec, which has the same semantics and can be used in Creusot, albeit being slightly less efficient (the content of the vector is first allocated in the stack, and then moved to the newly allocated vector, instead of being directly initialized in the heap). It needs to be explicitly imported in order to not conflict with Rust’s default implementation.

Command-line Interface

List of commands

Main commands

creusot

cargo creusot [--erasure-check] [-- [-p <CRATE>]]

Run the Creusot compiler.

Output Coma code in the verif/ directory.

Creusot options

  • --erasure-check: Report #[erasure] check failures as errors; see Erasure check.

    • --erasure-check=no: Disable #[erasure] checks.
    • --erasure-check=warn (default): Report #[erasure] check failures as warnings.

Cargo options

All options after -- are forwarded to cargo. Here is a selection of useful ones for Creusot users:

  • -p <CRATE>: Compile a specific crate <CRATE> in a multi-crate project.
  • -Zbuild-std: Recompile crates core, std, alloc, proc-macro. (Useful for --erasure-check.)

prove

cargo creusot prove [<PATTERNS>] [-i|--ide-on-fail|--ide-always] [--replay] [--why3session]

Verify contracts.

This first runs cargo creusot to be sure that the compiled code is up-to-date. Then why3find verifies the compiled Coma code: it generates verification conditions and tries to prove them.

Options

  • <PATTERNS>: Select Coma files that match one of the patterns. If no patterns are provided, prove all files. Example patterns: name, name::*, m/*/f. Separators can be written as :: or /.
  • -i, --ide-on-fail: Open the Why3 IDE on an unproved file to inspect its proof context.
  • --ide-always: Open the Why3 IDE on a single Coma file regardless of whether the proof succeeded. The command fails if <PATTERN> does not match exactly one file.
  • --replay: Don’t generate new proofs, only check if the existing proofs are valid.
  • --why3session: Generate why3session.xml files (implied by -i and --ide-always).

doc

cargo creusot doc

Build documentation.

This is a variant of cargo doc that also renders contracts (requires and ensures) and logic functions.

clean

cargo creusot clean [--force] [--dry-run]

Remove dangling proof files.

Removing (or renaming) Rust functions also removes (or renames) its compiled Coma file. However, the Creusot compiler can’t keep track of their associated proof files (proof.json, why3session.xml), which become dangling. cargo creusot will detect dangling files and print a warning to remind you to move those files if you want, otherwise you can remove them with cargo creusot clean.

Options

  • --force: Don’t ask for confirmation before removing dangling files.
  • --dry-run: Only print the list of files that would be removed by cargo creusot clean.

why3 ide

cargo creusot why3 ide <COMA_FILE|why3session.xml>

Run the Why3 IDE on a Coma file or a why3session.xml. This commands simply invokes why3 ide with the required options to load Coma files produced by Creusot.

This is a command for experts and for troubleshooting. In normal usage, prefer cargo creusot prove with -i or --ide-always, which ensures that the Coma artifacts are always up to date.

Create and maintain package

new

cargo creusot new <NAME> [--main] [--creusot-contracts <PATH>]

Create or update package named <NAME>.

Create directory <NAME> if it doesn’t already exist, and run cargo creusot init inside it.

Options

  • --main: Create main.rs for an executable crate. (By default, only a library crate lib.rs is created.)
  • --creusot-contracts <PATH>: Path to local creusot-contracts used to set the [patch.crates-io] section of Cargo.toml.

init

cargo creusot init [<NAME>] [--main]

Create or update package in the current directory.

If Cargo.toml doesn’t exist, create a new package with starting configuration and source files.

If Cargo.toml exists, update an existing package for verification with Creusot:

  • add or update creusot-contracts in the list of dependencies with the version matching your Creusot installation;

    For released versions of Creusot, this is equivalent to cargo add creusot-contracts@<VERSION> just with the right version.

    For a development version of Creusot (prerelease version -dev), this also adds the following lines:

    [patch.crates-io]
creusot-contracts = { path = "/path/to/creusot-contracts" }

    This setting is documented in The Cargo Book: Overriding Dependencies.

  • add why3find.json if it doesn’t exist.

Options

  • <NAME>: Name of the package. (By default, it is the name of the directory.)
  • --main: Create main.rs for an executable crate. (By default, only a library crate lib.rs is created.)
  • --creusot-contracts <PATH>: Path to local creusot-contracts used to set the [patch.crates-io] section of Cargo.toml.

Configuration

why3-conf

cargo creusot why3-conf [--provers-parallelism <N>]

Regenerate why3.conf (in $XDG_CONFIG_HOME/creusot/, by default on Linux .config/creusot/).

Options

  • --provers-parallelism: Set the max number of threads to use to invoke SMT provers. (Default: automatically detect the number of threads for your machine)

version

cargo creusot version

Print version of Creusot and accompanying tools.